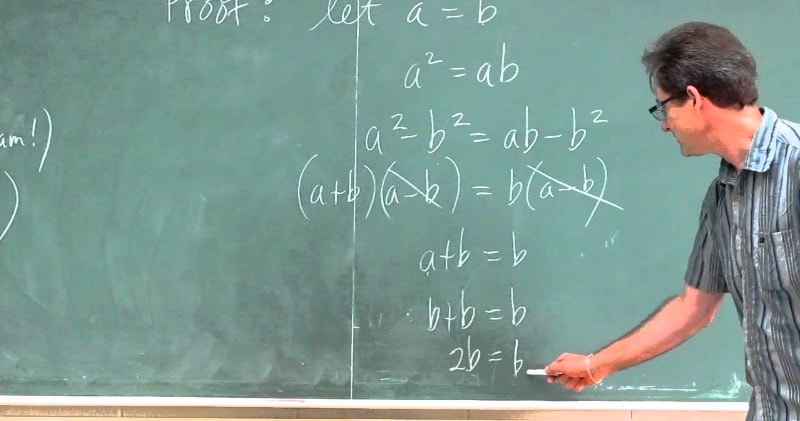Did you know that 1 = 2? Think that sounds ridiculous? OK, I’ll prove it to you. Then I’ll show you why this “proof” is indeed, as you suspected, ridiculous. And we’ll see what it all has to do with the number zero.
source/image: John Hush
Using algebra and a little deception, Mr. John Hush proves (or does he?) that 1 = 2 to a class of amazed calculus students.
Challenge your high school student to find the flaw in this short mathematical proof that one is equal to two. This activity provides a good review of basic math principals and the structure of mathematical proofs. It’s also a good reminder that knowing math principals is good protection against getting tricked.
Advertisement
Show your teen the proof.Ask her to tell you which step is invalid. She should determine both which number is wrong, and why.Help her keep going until she understands the answer./ read more (education)
The Proof that 2 = 1
1) Given
1) a = b
2) Multiply both sides by a
2) a2 = ab
3) Subtract b2 from both sides
3) a2-b2 = ab-b2
4) Factor both sides
4) (a+b)(a-b) = b(a-b)
5) Divide both sides by (a-b)
5) (a+b) = b
6) Substitute a for b
6) a+a = a
7) Addition
7) 2a = a
8) Divide both sides by a
8) 2 = 1
Solution:
Part one: Step five is wrong. The rules of mathematics do not allow us to divide by zero.
Since a and b are equal, (a-b) = 0. Therefore, we cannot divide by (a-b)!
Note: To explain why you can’t divide something by zero, ask your student how she would divide a pizza into 0 pieces. Impossible! The fewest number of pieces she could make would be one piece—the whole pizza!